湖北天健建设集团有限公司网站做网站需要准备什么
⾼精度
当数据的值特别⼤,各种类型都存不下的时候,此时就要⽤⾼精度算法来计算加减乘除:
- 先⽤字符串读⼊这个数,然后⽤数组逆序存储该数的每⼀位;
- 利⽤数组,模拟加减乘除运算的过程。
⾼精度算法本质上还是模拟算法,⽤代码模拟⼩学列竖式计算加减乘除的过程。
一、⾼精度加法
题⽬来源:洛⾕
题⽬链接:P1601 A+B Problem(高精) - 洛谷
难度系数:★
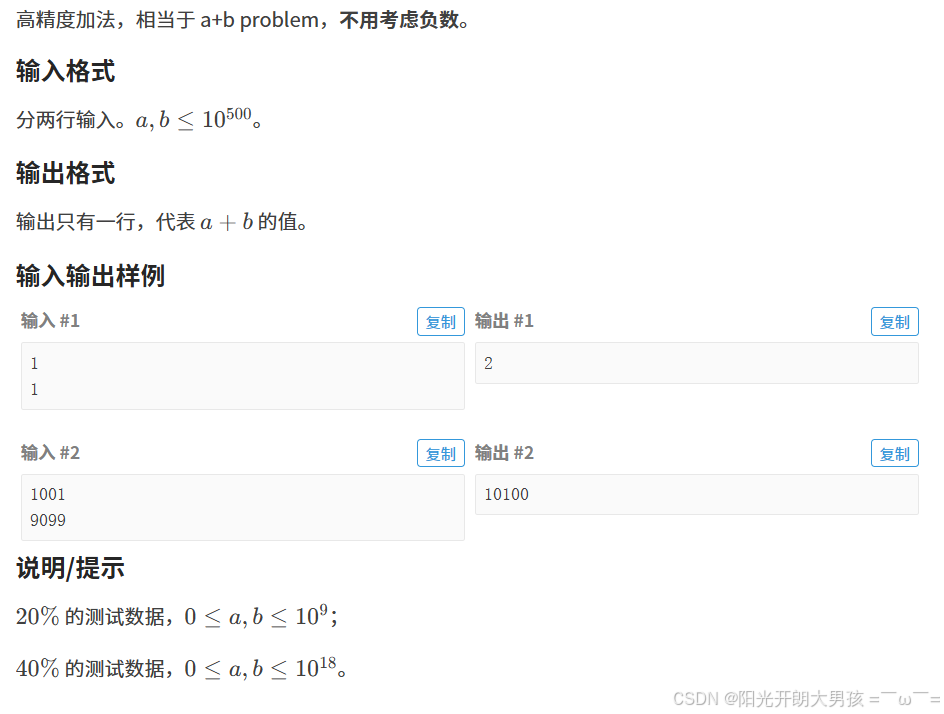
1. 题目描述
2. 算法原理
模拟⼩学「列竖式」计算「两数相加」的过程。
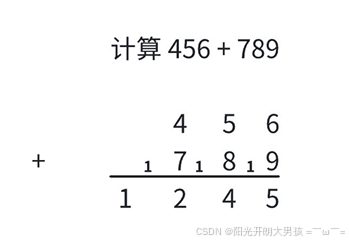
1. ⽤字符串读⼊数据;
2. 将字符串的每⼀位拆分,逆序放在数组中;
假设输入字符串“439”,通过x[i] - '0'转换成数字439,通过画图得出规律:一个数字在两个数组的代码下标和为n-1-i。
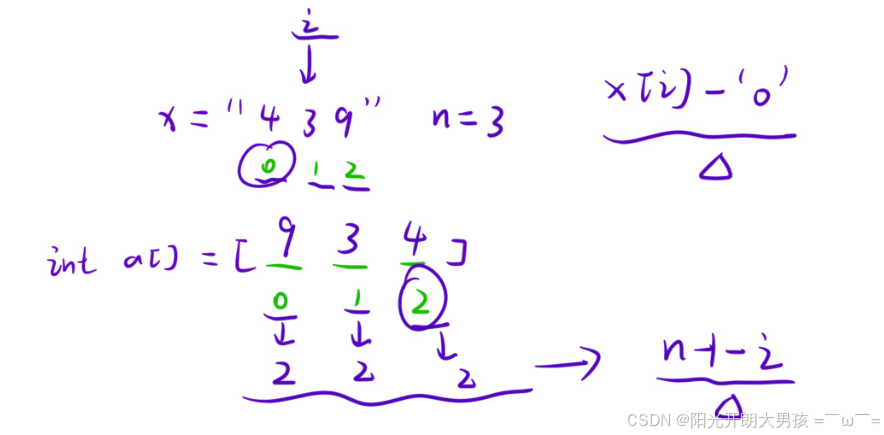
3. 模拟列竖式计算的过程:
- a. 对应位累加;
- b. 处理进位;
- c. 处理余数。

4. 处理结果的位数。
3. 参考代码
#include <iostream>using namespace std;const int N = 1e6 + 10;int a[N], b[N], c[N];
int la, lb, lc;// 高精度加法的模版 - c = a + b;
void add(int c[], int a[], int b[])
{for(int i = 0; i < lc; i++){c[i] += a[i] + b[i]; // 对应位相加,再加上进位c[i + 1] += c[i] / 10; // 处理进位c[i] %= 10; // 处理余数}if(c[lc]) lc++;
}int main()
{string x, y; cin >> x >> y;// 1. 拆分每一位,逆序放在数组中la = x.size(); lb = y.size(); lc = max(la, lb);for(int i = 0; i < la; i++) a[la - 1 - i] = x[i] - '0';for(int i = 0; i < lb; i++) b[lb - 1 - i] = y[i] - '0';// 2. 模拟加法的过程add(c, a, b); // c = a + b// 输出结果for(int i = lc - 1; i >= 0; i--) cout << c[i];return 0;
}二、⾼精度减法
题⽬来源:洛⾕
题⽬链接:P2142 高精度减法 - 洛谷
难度系数:★
1. 题目描述

2. 算法原理
模拟⼩学「列竖式」计算「两数相减」的过程。
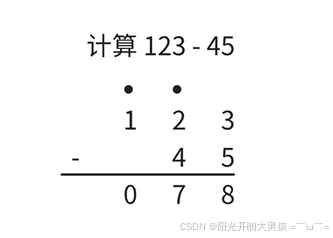
1. ⽤字符串读⼊数据;
2. 判断两个数的⼤⼩,让较⼤的数在前。注意字典序vs数的⼤⼩:
- a. 位数相等:按字典序⽐较;
- b. 位数不等:按照字符串的⻓度⽐较。
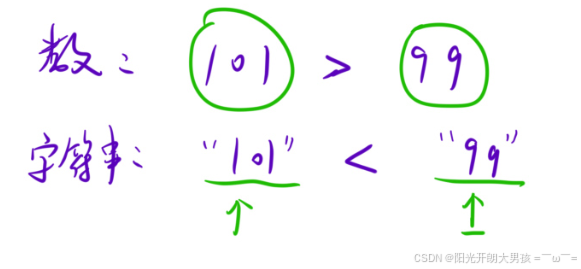
注意:字符串比较大小先看第一位
3. 将字符串的每⼀位拆分,逆序放在数组中;
4. 模拟列竖式计算的过程:
- a. 对应位相减求差;
- b. 处理借位(如果减的结果小于0往前借一位,然后这一位加上10);
5. 处理前导零。
如997-996 ,结果为001去掉多余的两个0,当结果为000时,结果取0
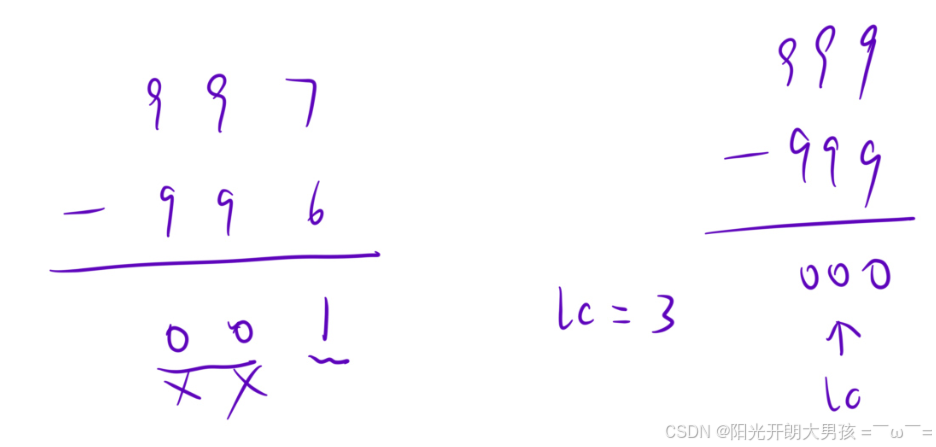
3.参考代码
#include <iostream>using namespace std;const int N = 1e6 + 10;int a[N], b[N], c[N];
int la, lb, lc;// 比大小
bool cmp(string& x, string& y)
{// 先比较长度if(x.size() != y.size()) return x.size() < y.size();// 再按照 字典序 的方式比较return x < y;
}// 高精度减法的模板 - c = a - b
void sub(int c[], int a[], int b[])
{for(int i = 0; i < lc; i++){c[i] += a[i] - b[i]; // 对应位相减,然后处理借位if(c[i] < 0){c[i + 1] -= 1; // 借位c[i] += 10;}}// 处理前导零while(lc > 1 && c[lc - 1] == 0) lc--;
}int main()
{string x, y; cin >> x >> y;// 比大小if(cmp(x, y)){swap(x, y);cout << '-';}// 1. 拆分每一位,然后逆序放在数组中la = x.size(); lb = y.size(); lc = max(la, lb);for(int i = 0; i < la; i++) a[la - i - 1] = x[i] - '0';for(int i = 0; i < lb; i++) b[lb - i - 1] = y[i] - '0';// 2. 模拟减法的过程sub(c, a, b); // c = a - b// 输出结果for(int i = lc - 1; i >= 0; i--) cout << c[i];return 0;
}三、⾼精度乘法
题⽬来源:洛⾕
题⽬链接:P1303 A*B Problem - 洛谷
难度系数:★
1. 题目描述
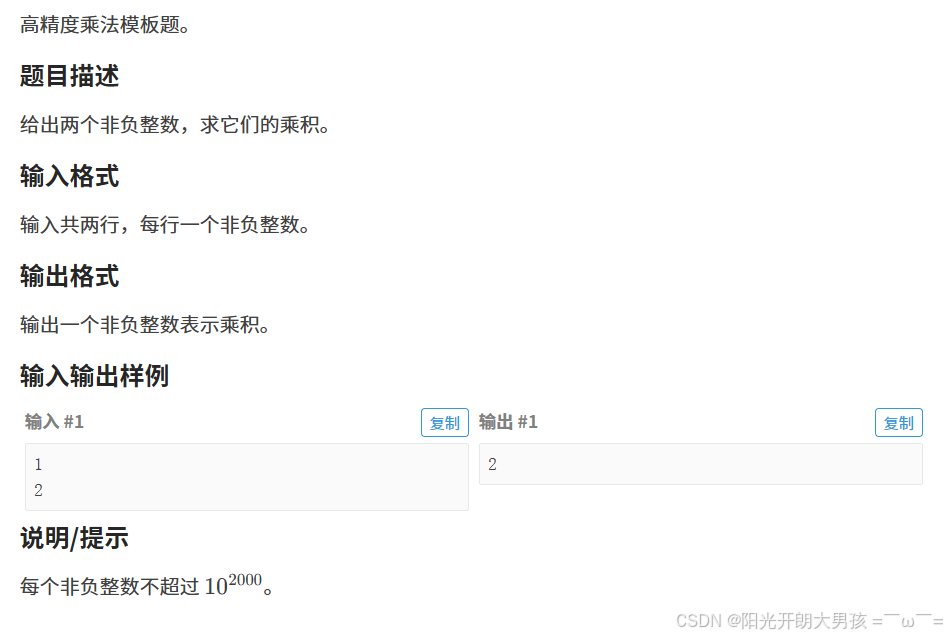
2. 算法原理
1. ⽤字符串读⼊数据;
2. 将字符串的每⼀位拆分,逆序放在数组中;
3. 模拟⽆进位相乘再相加的过程:
- a. 对应位求乘积;
- b. 乘完之后处理进位;
- c. 处理余数;
4. 处理前导零。
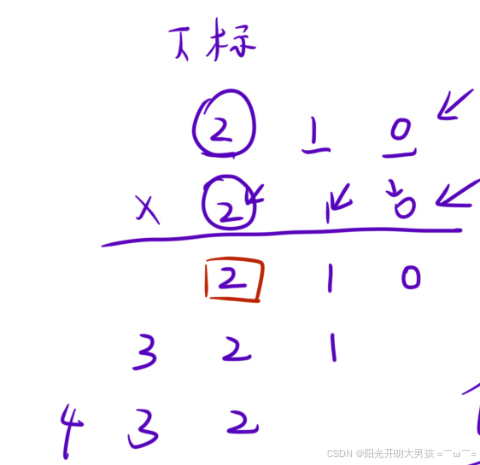
⽆进位相乘再相加:
- 还是「列竖式」,但是每⼀位相乘的时候不考虑进位,直接把乘的结果放在对应位上;
- 等到所有对应位置「乘完」并且「累加完」之后,「统⼀处理进位」。
如下图所⽰:
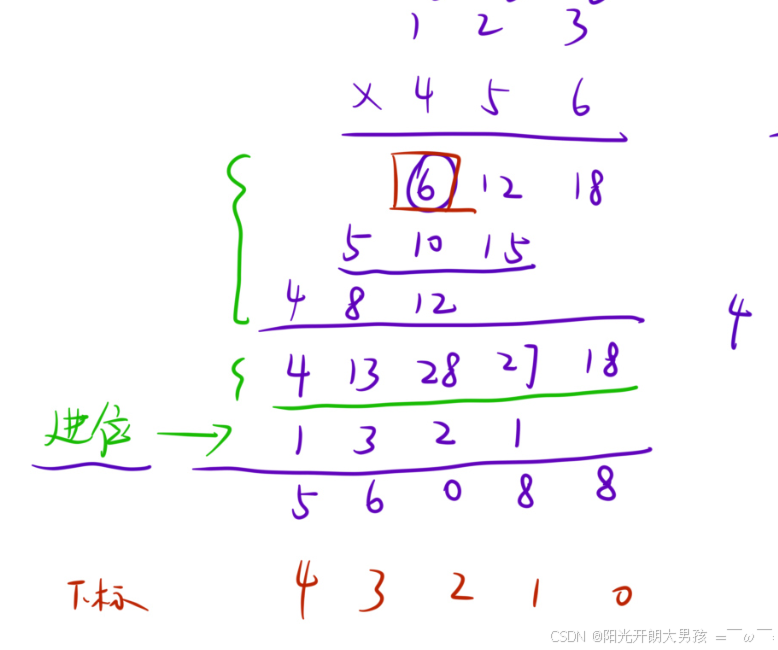
注意:与高精度加法、减法不同的是两个数(x,y)相乘最多会出现(x+y)位数 ,如最大的两位数99与最大的三位数999相乘的值为五位数98901。
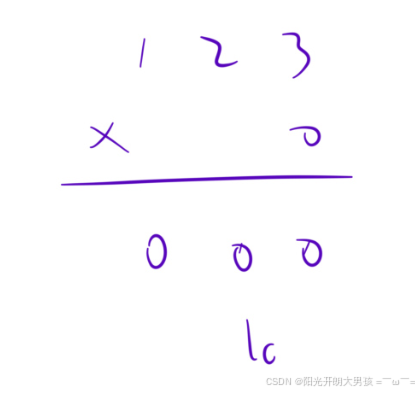
3. 参考代码
#include <iostream>using namespace std;const int N = 1e6 + 10;int a[N], b[N], c[N];
int la, lb, lc;// 高精度乘法的模版 - c = a * b
void mul(int c[], int a[], int b[])
{// 无进位相乘,然后相加for(int i = 0; i < la; i++){for(int j = 0; j < lb; j++){c[i + j] += a[i] * b[j];}}// 处理进位for(int i = 0; i < lc; i++){c[i + 1] += c[i] / 10;c[i] %= 10;}// 处理前导零while(lc > 1 && c[lc - 1] == 0) lc--;
}int main()
{string x, y; cin >> x >> y;// 1. 拆分每一位,逆序放在数组中la = x.size(); lb = y.size(); lc = la + lb;for(int i = 0; i < la; i++) a[la - 1 - i] = x[i] - '0';for(int i = 0; i < lb; i++) b[lb - 1 - i] = y[i] - '0';// 2. 模拟乘法的过程mul(c, a, b); // c = a * b// 输出结果for(int i = lc - 1; i >= 0; i--) cout << c[i];return 0;
}四、⾼精度除法
题⽬来源:洛⾕
题⽬链接:P1480 A/B Problem - 洛谷
难度系数:★
1. 题目描述
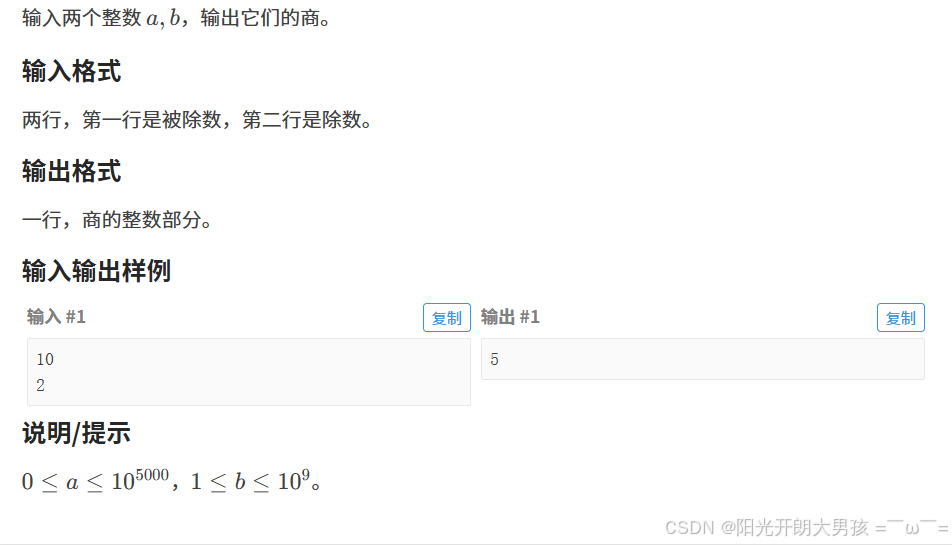
2. 算法原理
模拟⼩学「列竖式」计算「两数相除」的过程(注意,我们这⾥是「⾼精度÷低精度」)。
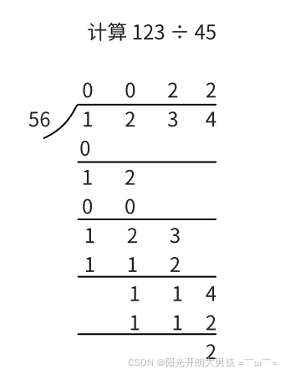
定义⼀个指针 i 从「⾼位」遍历被除数,⼀个变量 t 标记当前「被除的数」,记除数是 b;
- 更新⼀个当前被除的数 t =t×10+a[i] ;
- t/b表⽰这⼀位的商,t%b表⽰这⼀位的余数;
- ⽤ t 记录这⼀次的余数,遍历到下⼀位的时候重复上⾯的过程
被除数遍历完毕之后,t ⾥⾯存的就是余数,但是商可能存在前导 0 ,注意清空。

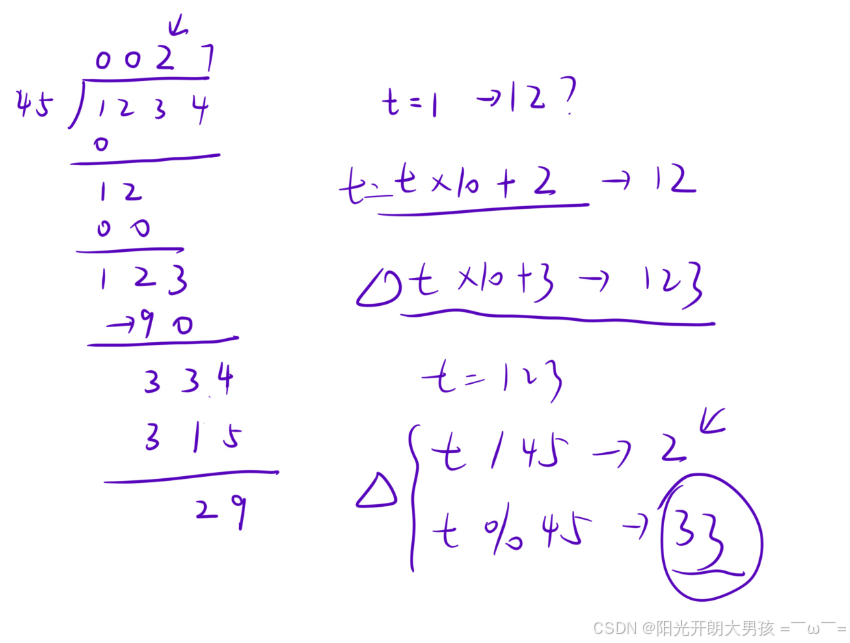
3. 参考代码
#include <iostream>using namespace std;const int N = 1e6 + 10;typedef long long LL;int a[N], b, c[N];
int la, lc;// 高精度除法的模板 - c = a / b (高精度 / 低精度)
void sub(int c[], int a[], int b)
{LL t = 0; // 标记每次除完之后的余数for(int i = la - 1; i >= 0; i--){// 计算当前的被除数t = t * 10 + a[i];c[i] = t / b;t %= b;}// 处理前导 0while(lc > 1 && c[lc - 1] == 0) lc--;
}int main()
{string x; cin >> x >> b;la = x.size();for(int i = 0; i < la; i++) a[la - 1 - i] = x[i] - '0';// 模拟除法的过程lc = la;sub(c, a, b); // c = a / bfor(int i = lc - 1; i >= 0; i--) cout << c[i];return 0;
}